Definitions of risk
There are many definitions of risk, they depend on specific applications and situational contexts. It can be assessed qualitatively or quantitatively.
Qualitatively, risk is considered proportional to the expected losses which can be caused by an event and to the probability of this event. The harsher the loss and the more likely the event, the greater the overall risk.
Frequently in the subject matter literature, risk is defined in pseudo-formal forms where the components of the definition are vague and ill defined, for example, risk is considered as an indicator of threat, or depends on threats, vulnerability, impact and uncertainty.
In engineering, the quantitative engineering definition of risk is: .
.
Independently on the wide use this definition, for example in nuclear energy and other potentially dangerous industries, measuring engineering risk is often difficult; the probability is assessed by the frequency of the past similar events, (or by event-tree methods) but rare failures are hard to estimate if an event tree cannot be formulated, and loss of human life is generally considered beyond estimation[citation needed] - however, radiological release (eg GBq of radio-Iodine) is usually used as a surrogate. There are many formal methods used to assess or to "measure" risk considered as one of the critical indicators important for human decision making.
Financial risk is often defined as the unexpected variability or volatility of returns, and thus includes both potential worse than expected as well as better than expected returns. References to negative risk below should be read as applying to positive impacts or opportunity (e.g. for loss read "loss or gain") unless the context precludes.
In statistics, risk is often mapped to the probability of some event which is seen as undesirable. Usually the probability of that event and some assessment of its expected harm must be combined into a believable scenario (an outcome) which combines the set of risk, regret and reward probabilities into an expected value for that outcome. (See also Expected utility)
Thus in statistical decision theory, the risk function of an estimator δ(x) for a parameter θ, calculated from some observables x; is defined as the expectation value of the loss function L,
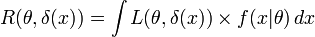
where:
- δ(x) = estimator
- θ = the parameter of the estimator
In information security, a "risk" is defined as a function of three variables:
- the probability that there's a threat
- the probability that there are any vulnerabilities
- the potential impact.
If any of these variables approaches zero, the overall risk approaches zero.
The management of actuarial risk is called risk management.
[ Source : Wikipedia]

 .
.